探索分割数组的方法（了解数组分割的常用技巧和策略）

数组是编程中常用的数据结构，经常需要对数组进行分割操作。本文将介绍一些常用的数组分割方法，帮助读者更好地理解和应用这些技巧和策略。

前缀和法（PrefixSum）

前缀和法是一种常见的数组分割方法，通过计算前缀和数组可以快速获取任意一个子数组的和。通过对原始数组进行预处理得到前缀和数组，可以在O(1)的时间复杂度内计算任意子数组的和。

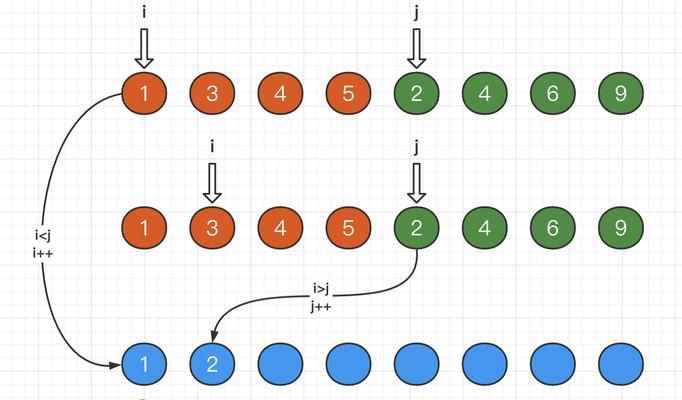
双指针法（TwoPointers）

双指针法是一种高效的数组分割方法，通过使用两个指针来遍历数组，可以在O(n)的时间复杂度内完成分割操作。双指针法常用于求解滑动窗口问题和排序问题。

二分法（BinarySearch）

二分法是一种常用的数组分割方法，通过在有序数组中查找目标元素的位置，可以将数组分割为两部分。二分法通常用于求解查找问题和区间划分问题。

动态规划法（DynamicProgramming）

动态规划法是一种递推的数组分割方法，通过将问题拆分为子问题并保存子问题的解，可以在O(n^2)的时间复杂度内完成分割操作。动态规划法常用于求解最优解和最长子序列等问题。

贪心法（GreedyAlgorithm）

贪心法是一种简单而有效的数组分割方法，通过每次选择当前最优解来逐步得到整体最优解。贪心法常用于求解最小生成树、最短路径等问题。

回溯法（Backtracking）

回溯法是一种递归的数组分割方法，通过不断尝试所有可能的分割方式来找到满足条件的解。回溯法常用于求解排列组合、子集和等问题。

分治法（DivideandConquer）

分治法是一种将问题分解为多个子问题并分别求解的数组分割方法，通过合并子问题的解来得到整体的解。分治法常用于求解排序、归并等问题。

滑动窗口法（SlidingWindow）

滑动窗口法是一种通过移动窗口来分割数组的方法，可以在O(n)的时间复杂度内完成分割操作。滑动窗口法常用于求解子数组最大值、最小值等问题。

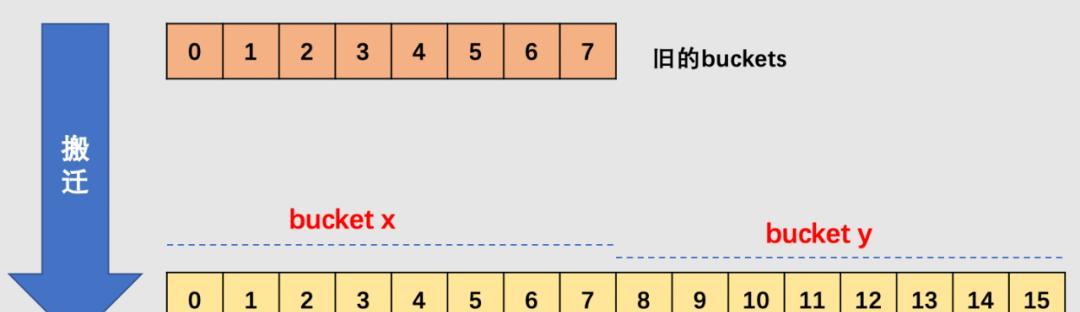
分块法（BlockDivision）

分块法是一种将数组划分为若干块，并对每一块进行预处理的分割方法，可以在O(n)的时间复杂度内完成分割操作。分块法常用于求解区间查询等问题。

位运算法（BitManipulation）

位运算法是一种利用位运算操作数组的方法，可以在O(n)的时间复杂度内完成分割操作。位运算法常用于求解数组中缺失数字、重复数字等问题。

随机化法（Randomization）

随机化法是一种通过随机选择元素进行数组分割的方法，可以在O(n)的时间复杂度内完成分割操作。随机化法常用于求解随机排列、蓄水池抽样等问题。

枚举法（Enumeration）

枚举法是一种穷举所有可能的数组分割方式的方法，可以在O(2^n)的时间复杂度内完成分割操作。枚举法常用于求解子集和、子序列等问题。

网络流法（NetworkFlow）

网络流法是一种将数组看作图进行分割的方法，可以在O(n^2)的时间复杂度内完成分割操作。网络流法常用于求解最大流、二分图匹配等问题。

线段树法（SegmentTree）

线段树法是一种通过构建线段树来进行数组分割的方法，可以在O(nlogn)的时间复杂度内完成分割操作。线段树法常用于求解区间查询、区间修改等问题。

数组分割是编程中常见的操作，我们介绍了15种常用的分割方法，包括前缀和法、双指针法、二分法、动态规划法、贪心法、回溯法、分治法、滑动窗口法、分块法、位运算法、随机化法、枚举法、网络流法和线段树法。不同的方法适用于不同的问题，我们需要根据具体情况选择合适的方法来进行数组分割操作。通过掌握这些方法，我们可以更加高效地解决数组分割问题。